摘要

本文建立了二阶和三阶Volterra时滞积分微分方程(VIDE)解一致渐近稳定的充分条件。在这里，我们证明了两个新的定理，它们是关于所考虑的VIDEs的解的UAS的。我们的方法是基于李亚普诺夫的第二种方法。我们的结果改进和形成一个补充，一些已知的最近的结果在文献中。用两个例子来支持结果，并绘制了两个图来说明所考虑的数值方程的零解的渐近稳定性。所得结果新颖新颖。

1 介绍

将微分方程与积分方程相结合的积分-微分方程近年来受到越来越多的关注。数学、物理、生物和工程中的应用都严重依赖于ide。

在20世纪早期，意大利数学家维托·沃尔泰拉研究了被称为沃尔泰拉方程的方程。在20世纪30年代，Volterra证明了一些季节性疾病(如流感)的数学模型可以用积分方程和微分方程来表示。VIDEs在生物学、生态学、医学、物理学和其他科学领域的应用非常广泛。据我们所知，它已经在各种物理应用中被观察到，包括玻璃形成过程，传热，一般扩散过程，中子扩散，不同产生率的生物物种共存，以及沙漠中的风波纹。

研究普通、泛函和ide解的定性特征的最重要的方法之一是李亚普诺夫第二方法，因为该方法被广泛认为是研究微分方程的一个极好的工具。从理论上讲，这种方法是非常重要的，它被用于许多不同的应用，参见[24]。Lyapunov的第二种方法是证明系统稳定性的充分条件，这意味着即使找不到Lyapunov- krasovskii泛函(LKF)候选项来推断系统的稳定性，系统仍可能是稳定的。

利用Lyapunov理论研究DDE解的行为，在文献中得到了许多有趣的结果，例如[4,10,15,16,22,25]。

此外，值得一提的是，根据我们对文献的观察，最近我们发现了许多关于这类视频的令人兴奋的论文，例如[2,3,9,10,11,12,13,15,16,17,18,19,20,21,22]。

2000年，Zhang[25]研究了线性标量VIDE的一致渐近稳定性

其中A是一个常数，是一个连续函数。

2015年Tunç[14]研究了具有时滞形式的非线性VIDE零解的稳定性和有界性

最近，Appleby和Reynold[1]在2022年研究了标量线性VIDE的渐近稳定性

本文的目标是对下列方程给出二阶和三阶带时滞的微分方程的微分方程存在的充分条件

(1.1)

和

(1.2)

式中分别为依赖于差的连续函数，和，为可积勒贝格函数的空间，为时滞与，也存在两个函数使得，与。函数和是定义在上的连续标量函数。

话1.1

我们将发表以下评论:

1 .:

每当，代入，代入Ax(t)，代入积分项，则(1.1)化简为[25]所考虑的方程。因此，(1.1)中得到的稳定性和结果包括并推广了前面的结果。

2 .:

在[1]中，如果用ax(t)代替项，并代入积分项，则(1.1)化简为[1]中考虑的方程。那么本文的稳定性结果包括并改进了文献[1]中得到的稳定性结果。然后(1.1)和式(1.2)对[1,25]中的结果进行推广和改进。

3 .:

作为物理中的一种应用，许多模型都可以通过ide建模。例如，首先，根据基尔霍夫第二定律，闭环的净电压降等于外加电压E(t)。因此，标准的闭合RLC电路可以由IDE控制[5]，其次，abel型Volterra积分方程描述了当传热被其辐射平衡时沿表面的温度分布。最后，abel型Volterra积分方程确定了半无限固体的温度，该固体表面可以通过非线性辐射散热[23]。

2 主要结果

考虑一般泛函微分系统

(2.1)

表示来自的函数。对于任意，我们指的是连续函数的空间。有什么标准吗?这个符号表示有一些。

这里，F是t的连续函数对于任何时间对于并且取闭有界集合为有界集合。

定理2.1

[7]为连续泛函和局部Lipschitz

。假设有一个连续函数满足

(i):

其中为楔形;

(二):

．

则式(2.1)的零解是一致渐近稳定的(UAS)。

下面两个定理将是(1.1)和式(1.2)的主要结果。

定理2.2

除了给出关于函数的基本假设外，对于(1.1)，我们假设存在非负常数，并且使得

(i):

和

(二):

和。

(3):

(四):

．

则式(1.1)的零解为UAS，设

定理2.3

结合函数和式(1.2)的基本条件，我们假设存在正常数和，因此下列假设成立

(i):

，和，。

(二):

和。

(3):

(四):

．

则式(1.2)的零解为UAS，设

3.定理的证明2.2。

将(1.1)重写如下

(3.1)

将LKF定义为

(3.2)

它可以写成

(3.3)

利用Schwarz不等式[8]，我们得到

利用这个不等式和前面的不等式，我们可以把(3.3)写成下面的形式

根据定理2.2的假设，我们有

其中W是一个楔函数。

因此，我们有

因此，我们可以得出这样的结论

(3.4)

另一方面

根据定理2.2的假设(i)，我们得出

(3.5)

因此，由(3.4)和式(3.5)，我们得出定理2.1的条件(i)是成立的。

现在，通过微分方程(3.2)，我们得到

从莱布尼茨规则[23]第17页和恒等式[23]第17页和[6]第41页，我们有

然后，我们得到

由条件(i)和不等式，我们得到

因此，我们得出结论

考虑条件(i) - (iv)和，我们有

因此，我们的结论是

(3.6)

在那里,

因此，由(3.4)、(3.5)和式(3.6)，定理2.1的所有假设都被满足。因此式(1.1)的零解为UAS。因此，定理2.2的证明现在已经完成了。

4 定理证明2.3。

我们可以将(1.2)重写为以下等效系统

(4.1)

将LKF定义为

(4.2)

由式(4.2)可得

应用条件(i)和不等式，我们得到

从条件(i)中，得到

(4.3)

根据Schwarz不等式[8]，我们有

应用定理2.3的条件，我们得到

由此得出

如果我们让

然后，我们得到

因为，我们有一个正常数，这样

(4.4)

现在，(4.2)变成

由(ii)，我们有，并由定理2.3的假设(i)，我们得出

(4.5)

LKF对t求导

从莱布尼茨规则[23]第17页和恒等式[6]第41页，我们得到

利用等效系统(4.1)，我们得到

从条件(i)，我们得到

由条件(iv)和不等式可知

因此，对于正常数，可以得出

(4.6)

由式(4.4)、(4.5)和(4.6)的结果可知，定理2.1的所有假设都满足，则式(1.2)的零解为UAS。

这样，定理2.3的证明就完成了。

目录

摘要
1 介绍
2 主要结果
3.定理证明 ink" data-track="click">2.2．
4 定理证明 ink" data-track="click">2.3．
5 说明性的例子
6 结论
参考文献

作者信息
道德声明



搜索
导航

#####

5 说明性的例子

例5.1

考虑下面的带延迟的视频

(5.1)

请注意,

所以，我们发现

和

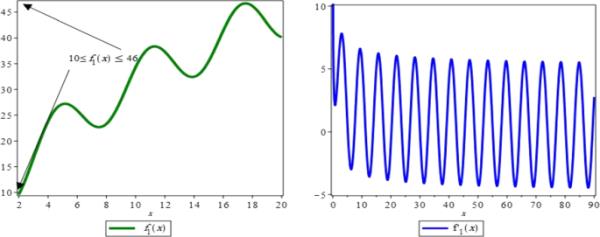
函数和的轨迹

图1分别显示了和在间隔和上的行为。

此外，我们有

和

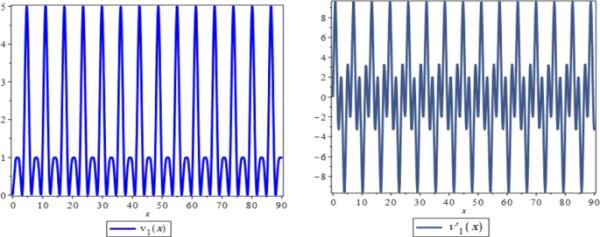
函数和的轨迹

图2显示了该区间的行为。

此外，我们还有

和

然后，我们得到

和

所以，很明显

我们可以从图3中看到解(x(t)， y(t))与(5.1)初值的行为。

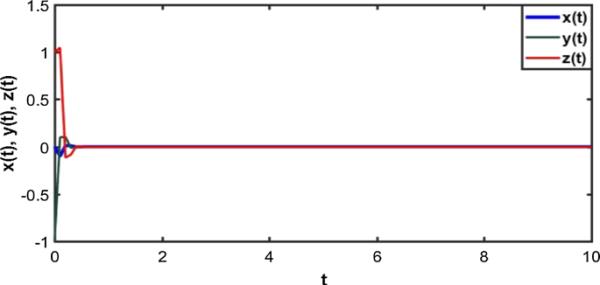
例5.1中解的轨迹

因此，定理2.2的所有假设都被满足。

则式(5.1)的零解为UAS。

例5.2

考虑下面的带延迟的视频

(5.2)

由此得出

所以，我们得到

和

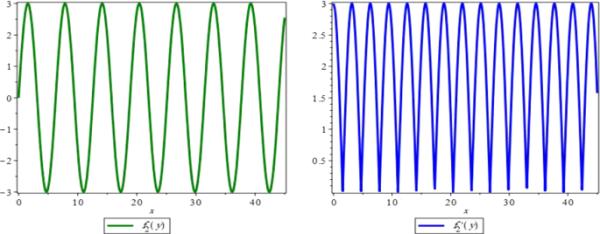
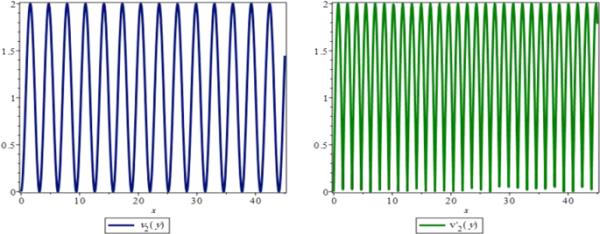
函数和的轨迹

图4显示了间隔和间隔上的行为。

此外

所以，我们得到

和

图5显示了间隔上的路径。

此外，我们还有

函数和的轨迹

和

此外，我们还有

和

所以，很明显

图6显示了解(x(t)， y(t)， z(t))在(5.2)的初始值下的行为。

例5.2解的路径

因此，定理2.3的所有假设都得到了验证。

则式(5.2)的零解为UAS。

6 结论

本文着重研究一类二阶和三阶非线性时滞VIDE解的稳定性。

利用Lyapunov的第二种方法，构造了一个合适的LKF，并用于建立定理2.2和2.3的充分条件。

给出了两个数值算例，并绘制了所有函数来证明定理2.2和2.3的充分条件，并在给定初始条件下绘制了数值解的轨道，以证明所得结果的有效性。

本文所得到的结果推广了许多已有的和令人振奋的关于非线性VIDE的结果。

下载原文档：https://link.springer.com/content/pdf/10.1007/s00009-023-02489-w.pdf