全闭环胰岛素输送系统改善T2DM患者血糖控制
17
2025-02-08
滞后期是在细菌生长过程中观察到的条件突然变化:生长受到抑制,而细胞适应环境。双相生长或双相生长通常在许多物种中表现出来。在两种糖存在的情况下,细胞最初通过消耗首选糖来生长,然后在第二种糖上恢复生长之前经历一个滞后期。生物量增加的特征是双增长曲线:指数增长之后是一段时间的不增长,然后是第二个指数增长。最近的文献缺乏完整的动态描述,人为地模拟滞后阶段,并采用前体池的非物理表示。在这里,我们制定了一个合理的机制模型,基于通量调节/蛋白质组分配与有限的前体池揭示核心机制紧凑的形式。与早期的系统不同,特征动力学作为解决方案的一部分出现,包括滞后阶段。重点是大肠杆菌在葡萄糖-乳糖混合物上的生长,我们展示了准确再现实验的结果。我们表明,对于单一菌株的大肠杆菌,双氧生长导致优化生物量产量。然而,有趣的是,对于两个相互竞争的菌株来说,共生生长并不总是最好的策略。我们的描述可以推广到多种不同的微生物模型和研究物种/菌株之间的竞争。
微生物细胞的生长表现为四个阶段:滞后、对数(指数)、平稳和死亡。当微生物受到条件的突然变化,例如引入新的生长介质时,观察到滞后期。在滞后期,细胞适应新环境,合成生长所需的细胞成分。
双氧生长(Diauxic growth)最早由Monod(1942, 1949)描述,当微生物被提供两种可以代谢的糖时,就会发生双氧生长。微生物首先消耗首选的糖,直到该来源几乎完全耗尽,然后才转向消耗第二种食物来源(Monod 1949)。在不同食物来源上,微生物生长的两个阶段之间存在一个滞后阶段,这似乎是在快速适应不断变化的生长条件和支持高(因此具有竞争力的)生长速度之间进行权衡的结果(Chu和Barnes 2016)。双重生长可以解释为在两种基质上最大化生长的一种方式(Kompala等人,1984;Salvy和Hatzimanikatis 2021):在广泛的条件下,基质的顺序使用而不是同时消耗是有益的(Chu和Barnes 2016)。然而,确切的条件尚不清楚,双氧生长比其他策略表现更好,例如同时消耗两种底物,尽管效率较低;在这两种资源都有限的竞争环境中,哪种压力总体上增长最快?
尽管已经确定了一些重要的调节过程,但控制微生物对条件变化的反应的潜在分子相互作用是复杂的。例如,只有当乳糖存在而葡萄糖(首选碳源)不存在时,大肠杆菌才会产生代谢乳糖的蛋白质。这是通过碳分解代谢抑制(CCR)和诱导剂排除来实现的。CCR是许多细菌中最重要的调控过程之一,占所有细菌基因的比例(Görke and st
葡萄糖的摄取抑制乳糖渗透酶将乳糖转运到细胞中的能力被称为诱导剂排斥(Aggarwal和Narang 2022)。磷酸转移酶系统(PTS)对葡萄糖的摄取伴随着去磷酸化酶EIIA的形成,EIIA通过与乳糖渗透酶结合而使其失活(Hogema et al. 1998)。
这两种调控机制之间基因表达水平的协同协调保证了优先碳源被使用,然后代谢被重新配置为使用次级碳源。
鸟苷3,5-二焦磷酸(ppGpp)下调核糖体的产生,上调氨基酸生物合成基因,已被发现在葡萄糖-乳糖二溶过程中基因表达的协调中起着重要作用(Traxler et al. 2006)。核糖体合成的调节,通过ppGpp,是由氨基酸需求和合成之间的平衡决定的。这种氨基酸通量已被确定为调节细菌生长速度的重要因素(Scott et al. 2014)。如上所述,cAMP在代谢调节中很重要,它协调分解代谢、生物合成和核糖体蛋白的表达,确保蛋白质组学资源在不同生长条件下根据需要用于不同的代谢部门(You et al. 2013)。
微生物中负责基因表达重组(资源分配)的机制通常被认为是通过进化优化的(Giordano et al. 2016)。最优机制取决于生长环境。例如,在非竞争环境中,增长产量的最大化被认为是一种优势(Giordano等人,2016),而当存在资源竞争时,增长速度的最大化将带来竞争优势(Ibarra等人,2002)。
最近关于资源配置的理论研究集中在增长率最大化上(Scott et al. 2014, 2010)。Scott等人(2014)使用细胞的粗粒度模型表明,通过最大化氨基酸通量,在核糖体蛋白部分的特定值上实现最大生长速率。假设细胞中蛋白质的数量不变,并将其划分为相关的部分(蛋白质组划分):核糖体蛋白和代谢蛋白。因此,增加核糖体的数量会降低代谢酶的水平。他们的优化控制策略基于氨基酸池大小,假设通过ppGpp发出信号,控制总蛋白质合成产生核糖体的比例(Scott et al. 2014)。类似的资源分配优化模型除了对蛋白质组的约束外,还包括能源约束(Maitra和Dill 2015;Weiße et al. 2015)。
上述研究涉及稳态模型,描述在很长一段时间内稳定的环境。然而,总体而言,微生物在其自然环境中受生长条件波动范围的影响。这推动了动态资源配置模型的制定(Salvy和Hatzimanikatis 2021;Giordano et al. 2016;Pavlov and Ehrenberg 2013;Erickson et al. 2017;Basan et al. 2020;Kremling et al. 2018)。Kremling等人(2018)提出了一个不同模型的集合,这些模型都表现出双声行为。通过定性比较模型预测,他们提供了对已提出的在CCR中发挥作用的各种机制的见解。Basan等人(2020)研究了两个单一碳源之间的转变,报告称长滞后阶段是由于关键代谢物的消耗和由此导致的代谢瓶颈。不同碳源对移位前生长速率的影响不同,序列通量限制模型预测了滞后时间与移位前生长速率之间的线性关系。Chu和Barnes(2016)提出的随机模拟模型表明,在不降低长期增长潜力的情况下,不可能缩短滞后期。次级代谢的过早激活缩短了滞后,但会给细胞带来成本,从而降低了在首选底物上的生长速度。他们通过模拟进化预测,在不太可能需要切换的环境中,滞后阶段会变长,而在频繁变化的环境中,滞后阶段会变短。Erickson等人(2017)提出了一种动态通量控制调节模型,该模型定量描述了基于蛋白质组资源动态再分配的适应动态。基因表达的时间演化是由调控函数决定的,调控函数的形式来源于稳态生长规律。这些调节函数的有效性存在局限性,此外,该模型预测生长速率和底物吸收率之间存在恒定的比例关系,这在滞后期生长过程中没有实验观察到。
在本研究中,我们扩展并修改了Erickson等人(2017)的模型,以包括对初始滞后期和双氧转换期间生物量增长和底物吸收的准确预测。我们开发了一个粗粒度模型,该模型使用分子过程的定性知识和通量平衡方法。我们明确地避免了其他模型(Salvy和Hatzimanikatis 2021)的潜在过度复杂性,因此我们没有大量不可测量的参数。模型描述中的未知动力学参数与可测量的动力学参数相关,以尽量减少拟合的需要。与许多描述滞后期的数学模型不同(Swinnen et al. 2004;Erickson et al. 2017),我们没有引入人工滞后参数来控制滞后的开始或长度。相反,滞后期的时间是由底物浓度和微生物蛋白质组的初始结构决定的。
我们提出了一个合理的描述,基于实验可测量的参数,它再现了大肠杆菌生长曲线的所有主要特征,从丰富的切换到最小的培养基和在葡萄糖-乳糖二溶。细菌生长的滞后期和对数期都是解决方案的一部分。这样的描述(在第2.3节中进行了总结)可以用来证明在整个成长期中二元增长的相对优点,并探索其他增长策略。
为了模拟通量控制调节(FCR),我们将采用Erickson等人(2017)的建模形式,开发一种合理的数学方法来解决建模不一致的问题,并扩展描述以描述前体和氨基酸池的物理方面。
Erickson等人(2017)提出的FCR模型描述了碳上升和下降过程中基因表达和生物量增长的时间演化。该模型通过改变平均翻译速率来平衡碳流入和蛋白质合成通量,平均翻译速率是由包括酮酸和氨基酸在内的中心前体池的大小决定的。产生哪些蛋白质(分解代谢酶/核糖体)是由调节功能决定的,其形式来源于稳态生长规律。该模型的中心假设是,在生长过渡期间调节函数的时间依赖性仅取决于转换速率的变化。
Erickson等人(2017)中定义的调节函数对于翻译率的特定值是未定义的,我们将其称为,并且对于不正确的调节函数是负的。的值虽然不会在稳态增长期间出现,但可能在增长过渡期间出现。为了消除这种不一致性并提供更坚实的理论基础,我们直接推导出与增长率的数学优化相关的调节函数(见第2.2.5节)。
原始的FCR模型(Erickson et al. 2017)指出,在感兴趣的时间尺度上,所有通量都是平衡的。这种平衡是通过假设翻译速率随着碳内流的任何变化而突然调整来实现的(由于底物可用性或关键酶浓度的变化)。然而,对于小的核糖体质量分数值或大的碳流入,这可能导致大的,物理上不切实际的翻译率。我们认为,由于翻译速率取决于前体池的大小,而前体池是有限的,所以翻译速率必须是有限的。因此,我们将把这个限制包括在我们的模型中(见第2.2.3节)。
此外,以上述方式要求通量平衡导致蛋白质合成速率和生物量增长率仅取决于分解代谢蛋白质量分数,核糖体质量分数从方程中消失。Erickson等人(2017)的模型所预测的生长速率与底物吸收率(恒定生物量产量)之间的恒定比例与实验观察结果不一致。我们在3.2.1节中提供的数据表明,在初始滞后阶段,生长速率与底物吸收率之比明显小于随后的对数生长阶段:生物量产量不是恒定的。这表明生长并不仅仅受到分解代谢蛋白的限制,因为这也会限制底物的吸收,而是必须取决于其他关键蛋白的水平。
在diauxie实验之前(详细描述见3.2.1节),大肠杆菌在含有碳源和生长必需氨基酸的Luria-Bertani肉汤(LB)上生长。在LB中生长的大肠杆菌细胞可以直接导入氨基酸,因此不需要使用合成代谢蛋白来构建氨基酸。事实上,实验已经发现,在LB中生长的大肠杆菌显示出许多与氨基酸生物合成途径相关的基因水平远低于在最小培养基中生长的大肠杆菌(Tao et al. 1999)。因此,我们提出,当大肠杆菌从富含LB的培养基转向最低限度的培养基生长时,发生的滞后期是由于缺乏氨基酸生物合成所需的合成代谢蛋白引起的。为了研究这一点,我们扩展了原始的FCR模型,以包括氨基酸合成通量。
外部底物被微生物x消耗,在微生物细胞内部,分解代谢酶将底物分解成前体。合成代谢蛋白结合前体形成氨基酸,这些氨基酸随后被核糖体结合成生长所需的蛋白质。所需的不同酶和蛋白质的相对量取决于生长条件和所消耗的底物。
我们构建了这一过程的数学描述,包括蛋白质组分配,通量控制调节和通过优化生长速率分配蛋白质合成。
使用已建立的蛋白质组分配模型(Scott et al. 2010;Scott and Hwa 2011),我们将细胞的总蛋白质含量分成不同的扇区,每个扇区由不同生长条件下表达水平具有相似生长速率依赖性的蛋白质组成。蛋白质组的生长速率依赖部分是核糖体相关蛋白质R,与碳输入和代谢相关的酶C,与氨基酸生产相关的合成代谢酶A,以及“非诱导”部分U, U通常随着生长速率的降低而减少(You et al. 2013)。蛋白质组的其余部分Q与生长速率无关,其质量分数非零且恒定。由此得出
(1)其中为部门i的质量分数。假设每个部门的最小质量分数与增长率无关(You et al. 2013),因此对于每个部门,增长率相关部分由。因此,对于质量分数中与增长率相关的部分,式(1)变为
这里是常数。注意到蛋白质组的未诱导部分与核糖体部分(在C和A限制下)相关,从而可以进一步简化这一点(You et al. 2013)。由此得出
(2)在细菌细胞生长的对数期,细胞增殖速率(growth rate)与关键蛋白的表达水平呈线性相关(You et al. 2013;Scott et al. 2010;Erickson et al. 2017)。假设每个蛋白质部门作为一个整体受到监管(You et al. 2013;Hui et al. 2015),因此与部门i中关键蛋白的表达水平成正比,因此与增长率成正比。用对数阶段质量分数的值表示如下
(3)其中为对数期大肠杆菌细胞的恒定生长速率,和为常数(详见附录A)。
我们的模型所代表的核心机制如图1所示。微生物吸收底物并将其分解成碳前体。这些前体与其他必需营养素结合起来,为细胞提供氨基酸库。核糖体利用氨基酸产生蛋白质z。蛋白质合成的速率取决于核糖体的浓度R和平均翻译速率,因此。蛋白质总质量占总生物量的比例相对恒定(Erickson et al. 2017)。因此,总生物量浓度X与总蛋白质浓度相关,其中常数p是生物量中蛋白质的比例。由此得出
(4)式中为蛋白质合成通量,与氨基酸合成通量类似的是,其中为氨基酸平均合成速率,为关键合成代谢蛋白的重标质量分数。(我们用比例因子重新调整,以从方程中去除未知常数,详细信息见附录a .3)。与总氨基酸部分的质量分数之间的关系,在附录的A.3节中讨论,Eq. (A3)给出了明确的依赖关系。
碳流入速率与底物吸收速率成正比。我们将底物吸收方程建立在Michaelis-Menten动力学基础上(详见附录B)。在有N个底物的情况下,我们有
(5)其中是特定底物分解代谢酶的重标质量分数,是特定底物上对数相生长期间该质量分数的值。(如前所述,我们重新调整以从方程中删除未知常数,详细信息见附录A.2。)对于非抑制酶,其中和。常数和分别为底物j的最大吸收速率和米凯利斯常数。
定义为碳前体的产率,由式(5)得到底物吸收速率,则由底物引起的碳流入速率为
(6)总碳通量。请注意,我们没有像Erickson等人(2017)那样假设这是恒定的,因为这将导致生物质产量恒定,这与实验观察结果不一致(如第2.1.1节所述)。在我们的模型中,因此,生物量产量取决于我们现在展示的生长条件和蛋白质组结构。
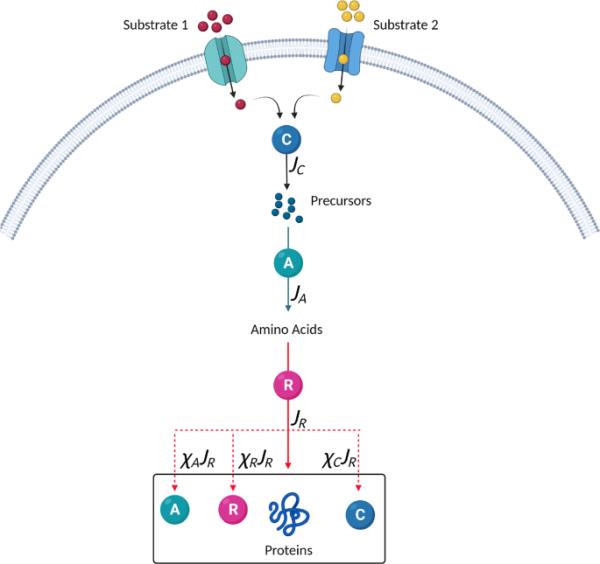
磁控调节模型。外部底物被吸收,然后被分解代谢酶(c区)分解,以提供碳前体池。底物和酶浓度的变化导致碳内流的变化。其他必需的营养物质,包括氮,与这些碳前体结合,由合成代谢蛋白(a区)合成,形成氨基酸。氨基酸合成的通量由。和之间的平衡是通过改变平均氨基酸合成速率来实现的,而氨基酸合成速率又取决于前体池的大小。在蛋白质合成过程中,氨基酸被核糖体(r区)“消耗”。蛋白质合成的通量由。和之间的平衡是通过改变平均翻译活性来实现的,这取决于氨基酸池的大小。调节功能,并决定核糖体,合成代谢和分解代谢蛋白,分别产生的数量。通过ppGpp和cAMP调节蛋白质合成的分配(Traxler et al. 2006;Scott et al. 2014;You et al. 2013),以响应前体和氨基酸库的变化。在给定的生长条件下,每种蛋白质都有一个使生长速度最大化的最佳水平。在生长过渡期间,蛋白质不在最佳水平,导致前体和氨基酸池的变化和非最佳生长速率。在模型中,直接推导出调节函数,并与增长率的数学优化相关联(图片由BioRender.com创建)(在线彩色图)
当生长条件发生变化时,可通过碳流入进入生长途径的碳量(如图1所示)受到影响。基材质量的突然上升可能会导致突然增加,从而导致碳前体的产量突然增加。a区蛋白的水平不会突然增加(因为蛋白质合成速率与生长速率成正比),生长途径会出现瓶颈。这可以通过突然增加氨基酸合成速率来解决,如Erickson等人(2017)所述,但以这种方式考虑大的变化需要为。相反,我们注意到前体池的大小受到细胞容量的限制,细胞内只有有限的空间。因此,碳前体的丰度是有限的,这取决于碳前体的丰度,反过来又限制了碳的价值。(类似地,翻译活动,将有一个最大值。)为了保持通量平衡,我们建议限制进入生长途径的碳。这是通过允许碳前体的产量随着生长条件的变化而变化来实现的。请注意,被分解但未进入生长途径的底物将作为产物释放(我们没有明确建模)。无论是恒定的(如Erickson等人(2017)),还是变化的(如本模型),都是如此。
我们用公式(6)中定义的通量表示添加到前体池中的碳前体的浓度,并表示随后由。因此,碳前体和氨基酸池的组合大小可以写成
(7)式中是从到的常数转换因子。细胞中可以维持的最大P值我们用K来表示,这个常数,K,类似于种群动力学中的承载能力,在给定的生长环境中可以维持的最大种群规模。在人口动态中,人口增长率受人口承载力的限制,随着人口规模向人口承载力靠拢,人口增长率趋于零。这里我们限制进入碳前驱体池的通量,以便。我们有
当给出时,基底j的碳通量是多少
常数是碳前体的产率,从。为了简化符号,我们引入函数
(8)如此......以至于......
(9)为了将模型中的变量数量保持在最小,我们希望仅根据底物浓度和蛋白质质量分数来定义碳流入。这意味着我们需要知道P,因此,只根据底物浓度和蛋白质质量分数。这是通过考虑通量平衡来实现的。
如第2.2.2节所述,氨基酸合成通量由中给出,其中取决于碳前体的丰度。为简单起见,我们取一个线性相关的设定,其中,的吸收率是一个常数。由底物j引起的氨基酸合成通量由下式给出。同理,取总蛋白质合成通量,其中常数为对蛋白质的摄取速率,常数为从蛋白质到蛋白质的转换因子,得到由于底物j的蛋白质合成通量。
和的变化率用通量表示,和由
为了达到通量平衡,假定和的变化发生在一个相对较快的时间尺度上,因此。本质上,这意味着在感兴趣的时间尺度上,所有的通量都是平衡的
(10)将和代入式(10)中,得到一个2N个以和为形式的方程组。这些可以求解得到底物浓度和蛋白质质量分数。从这些我们可以算出P,用式(7),把P代入式(9)得到
(11)式中和分别为仅消耗底物n时的最大翻译速率和最大氨基酸合成速率。(11)式推导的全部细节见附录C。
将式(11)与式(6)给出的定义进行比较,可以得出
(12)这个方程描述了碳前体的产率如何随着底物浓度(通过)和蛋白质质量分数的变化而变化。
我们现在使用公式(11)和通量平衡方程(10)推导出生物量增长方程。
用蛋白质合成通量表示的生物量增长方程如式(4)所示。从通量平衡我们得到,由式(11)所示。由此得出
(13),由式(8)给出
(14)与底物吸收率不成正比,取决于每个依赖生长的蛋白质组部分的质量分数。对于small,增长率受到限制,对于and (through)也是如此。至关重要的是,对于固定的底物浓度(常数),生长速率在特定值,和时具有唯一的最大值。我们假设在对数相期间细胞以这种最佳速率生长。这个假设唯一地定义了方程中未知常数的值。(13)、(14)、(后一种常数的组合出现在定义中)。根据实验可测量的参数,我们发现
(15) (16) (17)其中常数是在基质j上对数阶段生长期间测量的生物量产量。详细信息见附录D。
通过ppGpp和cAMP调节蛋白质合成的分配,以响应前体和氨基酸库的变化(Traxler et al. 2006;Scott et al. 2014;你等人。2013):蛋白质水平调整,直到池的大小是最佳的。池大小的变化表现为生长速率的变化(前体和氨基酸池的大小明确包含在生长速率方程的推导中(14),参见2.2.3节),因此,当前体和氨基酸池大小最优时,生长速率最大。因此,我们通过调节蛋白质水平的调节功能来分配蛋白质合成通量,直到生长速度达到最大。
属于蛋白质组生长独立部分的蛋白质Q,作为总蛋白质产量的恒定分数,产生。属于生长依赖性蛋白质组部门的蛋白质根据蛋白质组的当前状态和生长条件产生不同数量的蛋白质。蛋白质组的R、A和C部分分别由生长独立部分和生长依赖部分组成。对于生长依赖的部分,我们定义了调节函数,并分别表示r -扇区、c -扇区和a -扇区蛋白质在总蛋白质产量中的比例,以便
(18a) (18b) (18c)随着蛋白质总量的增加,调控功能受到
(19)我们还需要,因为蛋白质不会被回收或破坏(这是我们模型的一个简化假设)。利用2.2.2节中给出的生物量浓度与总蛋白质浓度、蛋白质浓度与蛋白质质量分数之间的关系,我们根据生长依赖的蛋白质质量分数(详见附录E)重写了公式(18)
(20a) (20b) (20c)增长率,,由式(14)给出。底物特异性酶属于C区,因此它们的调控取决于。我们设置
(21)式中为底物特异性酶的调控功能。对于总是与整个C区成比例表达的酶,然而,如果酶在某些条件下被抑制,情况就不是这样了。我们在这里设置
(22)其中函数从最大级别,for切换到for。的选择
(23)其中,便于这样的切换顺利进行(for we have and for we have)。功能取决于系统中存在哪些底物,并决定底物特异性酶是否被表达。例如,当模拟葡萄糖-乳糖二溶时,葡萄糖特异性酶将总是被表达,因此我们设置(也注意,当酶总是被表达时,我们有和因此)。然而,乳糖特异性酶只有在葡萄糖浓度充分下降时才会表达。乳糖摄取开启的时间点还没有很好的定义,但我们需要当葡萄糖浓度很大时。这可以通过设置来建模
(24)式中为常数,给出在葡萄糖存在下乳糖特异性酶的表达水平(表达前水平)。这种功能的选择使葡萄糖浓度高时抑制乳糖摄取和葡萄糖浓度为零时不抑制乳糖摄取之间的平稳过渡成为可能。葡萄糖水平必须下降,以便在乳糖特异性酶完全表达之前。Okano等人(2020)使用了类似的功能形式来模拟大肠杆菌对底物的分层使用中的酶调节。
如上所述,我们需要模型中的调节功能来调节蛋白质水平,直到在给定条件下,即底物浓度,生长速度最大化。为了导出调节函数,我们利用标准微积分的结果,即函数在给定点的最大增长率是在该函数在该点的梯度所给出的方向上。当调节函数受到约束时,我们设置
(25a) (25b) (25c)满足式(19)。选择该功能是为了确保,并且不会单独超过,选择该功能是为了确保,并且。和的推导的详细内容载于附录F。
这些调节功能是通过ppGpp和cAMP进行的蛋白质合成调节的数学表示:在给定环境中调节蛋白质水平以优化生长速率。调节函数永远不会是负的,并且总是满足式(19)给出的对蛋白质产量的约束。
因为它的值是由式(2)决定的,所以从这里起,我们就不显式地求解了。
综上所述,我们建立了一个机制模型,描述了碳上升和下降过程中生物量增长、底物浓度和基因表达的时间演化。微生物生长的阶段来自蛋白质组的动态,而不是在特定的时间打开/关闭。该模型结合了蛋白质组分配、通量控制调节和蛋白质合成的最佳分配。控制方程是
(26a) (26b) (26c) (26d)与增长率,,由式(14)给出。表1和表2给出了模型变量和参数的概述。
抑制底物摄取的确切机制在模型中不明确,使其灵活并适用于许多过程。此外,该描述可以推广到多种不同的微生物模型,便于研究不同物种或菌株之间的竞争。
该模型可用于描述由缺乏核糖体蛋白、无代谢蛋白或分解代谢蛋白引起的滞后期。事实上,与之前发表的模型不同(Erickson et al. 2017;Salvy and Hatzimanikatis 2021;Wu et al. 2023),该模型可以捕获更复杂的系统,其中存在连续滞后阶段,例如,由于生长培养基从丰富到最少(缺乏合成代谢蛋白)的变化而产生的初始滞后,然后是双氧化转变(缺乏特定的分解代谢蛋白)。
我们现在将我们的模型应用于大肠杆菌在葡萄糖-乳糖混合物上生长的特殊情况,将数值结果与文献数据和初步实验数据进行比较。
我们首先使用Erickson等人(2017)的大肠杆菌葡萄糖-乳糖二溶实验数据参数化并测试我们的数学模型。然后,我们根据自己的实验数据测试该模型,除了葡萄糖-乳糖双氧转换外,还包括由于从丰富到最小生长介质变化而产生的初始滞后。
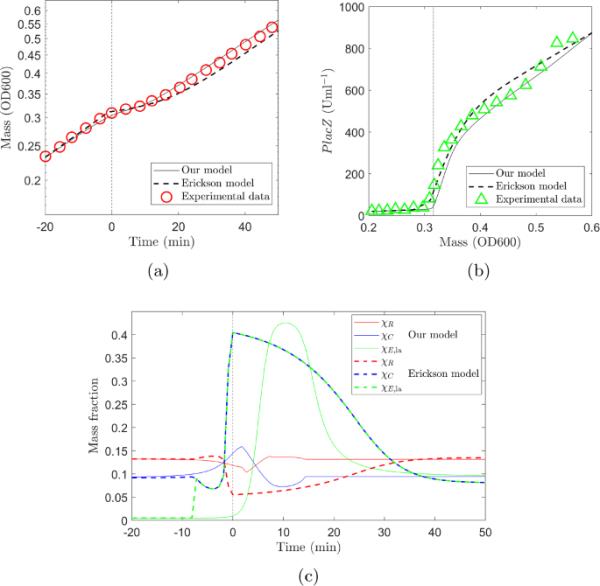
将我们的模型与Erickson等人(2017)的模型的模拟结果与Erickson等人(2017)的图3的实验数据进行比较。大肠杆菌在葡萄糖和乳糖上的生长曲线。黑色实线表示我们模型的结果,黑色虚线表示使用Erickson模型的结果(Erickson et al. 2017),红色圆圈表示实验数据。b乳糖特异性分解代谢酶PlacZ的表达水平。黑色实线表示我们模型的结果,黑色虚线表示使用Erickson模型的结果(Erickson et al. 2017),绿色三角形表示实验数据。c两种模型的调节功能比较。实线表示该模型,虚线表示Erickson模型。这两种模式的主要区别在于在双声速转换点对C扇区的调节。在我们的模型中,酶生产的大规模升级只影响乳糖特异性酶,而在埃里克森模型中,整个C部门都被上调。垂直虚线表示对偶位移(联机彩色图)
我们模拟了在葡萄糖和乳糖混合物上生长的大肠杆菌的双氧转移,并将我们的结果与Erickson等人(2017)的实验数据进行了比较。数值模拟中使用的控制方程和参数的详细信息见附录g。使用求解器ode15在Matlab (Matlab 2020)中求解方程。
图2显示了我们模型的模拟结果,我们使用Erickson等人(2017)的模型再现了模拟结果,并从Erickson等人(2017)的图3中获取了实验数据。图2a显示了大肠杆菌在葡萄糖和乳糖上的生长曲线。我们的模型结果用黑色实线表示,黑色虚线表示使用Erickson模型的结果(Erickson et al. 2017),红色圆圈表示实验数据。我们在这里再现的Erickson模型的结果与Erickson等人(2017)的图3所示的结果存在差异。这是由于我们已经纠正的原始工作中比例因子的错误计算(Erickson等人(2017)的图3的标题中引用的移位后立即的预测响应7866 UmlOD600应该是8280UmlOD600)。图2b显示乳糖特异性分解代谢酶PlacZ的表达水平。黑色实线表示我们模型的结果,黑色虚线表示使用Erickson模型的结果(Erickson et al. 2017),绿色三角形表示实验数据。PlacZ的表达在葡萄糖存在时被抑制,但在葡萄糖消耗时迅速增加,这发生在垂直虚线所示的位置。两种模型的调节函数对比如图2c所示。实线表示我们模型的调节功能,虚线表示Erickson模型(红色),(蓝色)和(绿色)。这两种模式的主要区别在于在双声速转换点对C扇区的调节。在我们的模型中,酶生产的大规模升级只影响乳糖特异性酶,而在埃里克森模型中,整个C部门都被上调。
结果表明,两种模型均能较好地再现生长曲线和酶表达水平,其中我们的模型与生长曲线数据(我们的模型和Erickson模型的残差平方和)拟合略好,Erickson模型与PlacZ表达水平(我们的模型和Erickson模型的残差平方和)拟合略好。
我们现在用我们的模型来描述一个更复杂的实验系统,其中有两个连续的滞后阶段:最初的滞后是由于从丰富的生长介质到最小的生长介质的变化,然后是二元转移。为了准确地预测这样一个系统中生物量和底物浓度的时间演变,模型必须包括多个蛋白质组部门和可变的生物量产量。这些特征包含在我们的模型中,不像以前发表的模型(Pavlov和Ehrenberg 2013;Erickson et al. 2017;Salvy和Hatzimanikatis 2021),因此无法对该系统进行建模。
我们使用混合大肠杆菌菌株重现了Mostovenko等人(2011)的葡萄糖-乳糖二溶实验。采用以下两株菌株:大肠杆菌MV1717 (MG1655 lac含有染色体编码、诱导CDI-msfGfp、氯霉素(Cm)抗性)和大肠杆菌MV1300 (MG1655 delta lacZYA;卡那霉素(Kan)耐药。菌株MV1717可以在乳糖(lac)上生长,而MV1300不能利用乳糖(lac),因为它缺少编码乳糖渗透酶的lacY基因,乳糖渗透酶是一种将乳糖泵入细胞的膜转运体。在MacConkey琼脂上的生长证实了这一特性,如图3所示,MV1717 (lac)菌落生长为粉红色,而MV1300 (lac)菌落生长为无色(白色)。
这两种实验都利用了在差异麦康基琼脂上生长的大肠杆菌菌株。乳糖发酵罐会长成红色或粉红色,不能利用乳糖的细胞不会改变颜色。左图:MV1717是一种乳糖发酵菌株。右图:MV1300一种非乳糖利用(lac)菌株(在线彩色图)
菌株在Luria-Bertani琼脂(LB-agar Miller)上单独培养过夜;LMM0204, Formedium, Hunstanton, UK), 37°C。然后,每个菌株的单个菌落在50 mL Falcon试管中培养过夜,其中含有25 mL LB培养基(LB broth, Miller;BP9723-500, Fisher BioReagents, Loughborough, UK), 37°C, 120 rpm轨道振动。LB-琼脂和LB肉汤均含有抗生素:MV1300为30 g/mL Kan, MV1717为34 g/mL Cm。使用抗生素是必要的qPCR我们进行的目标质粒这些菌株携带用于定量。
利用已建立的大肠杆菌OD与细胞密度关系测量生物量(Brown 2010)。(请注意,虽然OD可能取决于细胞的几何形状、粒度和其他方面,但通常假设OD与生物量成正比。)当600 nm光密度(OD600)达到1.4 (cells/mL)时,在g, 37℃下离心(离心机5810 R, Eppendorf),收获每个试管的生物量。去除上清,将微球重悬于10ml温(37°C)过滤无菌的1x磷酸盐缓冲盐水(PBS 20-7400-10, Severn Biotech Ltd.)中。以相同的参数再次纺丝。除去PBS,将颗粒重悬于10ml的1x morpholinepropanesulonic acid (MOPS)微量培养基(Teknova, Hollister, CA, USA)中。
接种前以1:1的比例(v/v)混合,测定接种量OD600(接种量OD600为6.82)。混合培养用于接种一个3l的玻璃高压灭菌生物反应器(Applikon Biotechnology, Delft, Netherlands),其中1l的1x MOPS最小培养基(Teknova, Hollister, CA, USA)含有0.5 g/L葡萄糖和1.5 g/L乳糖作为唯一的碳源(Traxler et al. 2006;Mostovenko et al. 2011)。通过循环水浴(OLS200, Grant Instruments)将生物反应器温度维持在37°C(°C)。通过生物控制器(ADI 1010, Applikon Biotechnology, Delft, Netherlands)监测和记录培养pH,并通过添加2m NaOH来维持pH。通过在270 - 500 rpm范围内调节搅拌速度(马达控制器,ADI 110, Applikon Biotechnology, Delft,荷兰),并使用固定的1 L/min空气流量(Traxler等人,2006),将溶解氧保持在20%以上的饱和度。
如Mostovenko等人(2011)所述,为了监测细胞密度、葡萄糖和乳糖浓度,在双氧移前后每30分钟、在双氧移前后每10分钟采集2 mL样本。使用Thermo Spectronic Biomate 3紫外可见分光光度计(ThermoFisher Scientific, UK)对未接种的生长培养基空白进行调零,通过评估OD600来测量大肠杆菌的生长。对于较大的OD600值(),我们根据在介质中稀释并重新测量的样品计算OD600。葡萄糖和乳糖浓度采用酶促试剂盒(分别为CBA086, Sigma-Aldrich和K624, BioVision)测定。等份细胞也在MacConkey琼脂上培养,37℃孵育过夜,用于乳糖和非乳糖发酵菌株的分化和计数。
细胞密度和葡萄糖和乳糖浓度的测量可以准确地确定初始滞后期(由从富LB培养基到最低培养基的生长切换引起)和双氧生长的开始,见图4。
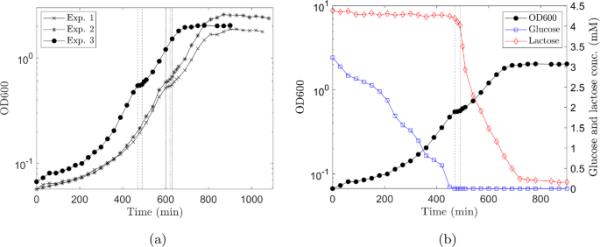
混合大肠杆菌菌株对葡萄糖和乳糖的双重生长特征。a三个独立生物复制的生长曲线,说明在初始滞后期,由于双氧转移的滞后期和所有糖消耗时的稳定期之间的过渡。b重复实验3中与生长曲线不同部分相关的葡萄糖和乳糖浓度;黑线和圆圈在a中,为了完整,这里再次显示。葡萄糖(蓝线,方形)最初被两种菌株(MV1717, MV1300)消耗,然后进入由双氧转向乳糖发酵引起的滞后期。垂直虚线表示双移通道(在线彩色图)
在最初的滞后阶段(最多约200分钟),底物被吸收(葡萄糖水平下降;如图4b中蓝线和方框所示),但增长率明显小于(图4b中生长曲线的梯度,即黑线和圆圈,min比min小得多)。实验1和2中观察到的较长的初始滞后期可能是由于用于接种实验1和2的两种培养物(接种后20小时)比实验3(接种后18小时)稍老。diauxxie开始于培养达到OD600或密度约为细胞/mL时(Brown 2010),并在生长曲线上出现一个最小平台期(图4)。diauxxie位移的OD600在三个实验中是相似的(OD600为0.52,0.59,0.55),见图4a和Mostovenko等人(2011)。diauxie的发生与生长介质中葡萄糖的耗尽相对应。乳糖在双氧转换后250 min左右被耗尽,OD600时达到生长稳定期。qPCR的数据表明,当培养基中有葡萄糖时,MV1717和MV1300的数量大致相等,但只有MV1717在转换为发酵乳糖的滞后期后继续生长,见图5。一旦糖源耗尽,这些细胞就会进入静止期。
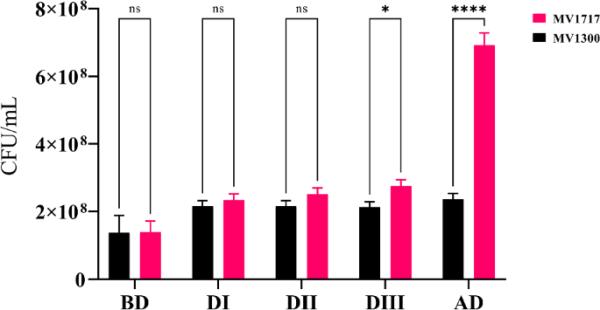
麦康基琼脂上乳糖(MV1717)和非乳糖(MV13000)发酵菌株的计数。BD =双声移前(420 min)呈指数增长的样品;DI-DIII =双声位移(分别为470,480和490 min)期间的样品;AD =双氧移后和指数生长期间的样品(600 min)。柱状图表示三个重复的标准差(n = 3)。差异的显著性采用双因素方差分析(****;使用GraphPad Prism软件9.0.2版本(Motulsky 2021)(在线彩色图)
这些结果清楚地表明,滞后阶段与从富培养基切换到最低培养基和葡萄糖/乳糖双重作用有关。当细胞转换代谢途径时,生长被中断,然后恢复。
我们有两种不同浓度的大肠杆菌,其中一种不能在乳糖上生长。两种菌株最初都在富培养基(LB肉汤)上生长。然后将菌株以1:1的比例混合,并转移到含有葡萄糖(0.5g/L)和乳糖(1.5g/L)混合物的最小培养基中,作为唯一的碳源。葡萄糖、乳糖和总生物量的浓度测量,从菌株转移到最小培养基的点开始,每隔一段时间进行一次。
数值模拟中使用的控制方程和参数的详细信息见附录h。在Matlab (Matlab 2020)中使用求解器ode15对方程进行求解。图6a中的实线显示了预测的糖浓度和总生物量随时间的变化,实验数据(以十字表示)被绘制出来进行比较。两个菌株的蛋白质组区质量分数如图6b所示。

混合大肠杆菌菌株对葡萄糖和乳糖的双重生长特征。实线表示葡萄糖(蓝色)和乳糖(红色)浓度和生长曲线(黑色)的数值预测。实验数据(图4中实验3)用叉表示。生长曲线为两菌株生物量之和,。该模型预测了一系列政权。最初,即使基质被吸收,生物量的增长也非常缓慢,这与实验数据很好地吻合。在8 h左右的预测生长曲线上可以明显地看到二元位移,与实验结果一致。b菌株1(实线)和菌株2(虚线)的r区蛋白(蓝色)、c区蛋白(红色)、乳糖特异性酶(洋红色)和a区蛋白(绿色)的质量分数。a区蛋白()的初始低水平导致生长缓慢,并且由于蛋白质产量与生长速率成正比,蛋白质质量分数的变化缓慢。随着生长速率的增加,质量分数向葡萄糖消耗的最佳水平移动。当葡萄糖消耗殆尽,其蛋白质质量分数停止变化时,菌株2就停止生长。菌株1开始消耗乳糖,并重新调整其蛋白质质量分数,最明显的是乳糖特异性酶的水平,以达到乳糖消耗的最佳水平。当乳糖耗尽时,菌株1停止生长,大约在12小时,它的蛋白质质量分数停止变化(在线色图)
该模型预测,即使基质被吸收,初始生物量增长也非常缓慢,这与实验数据很好地吻合。最初的缓慢生长是由于蛋白质质量分数在最小的培养基中在葡萄糖上生长的非最佳水平。之前在富培养基中生长的菌株具有低水平的合成代谢a区蛋白,因此很小(见图6b),导致生长缓慢。随着生长速率的增加,质量分数向葡萄糖消耗的最佳水平移动。当葡萄糖耗尽时,菌株2停止生长,其蛋白质质量分数停止变化。菌株1的蛋白质质量分数,特别是乳糖特异性酶的蛋白质质量分数,处于乳糖消耗的非最佳水平,其生长减慢,即滞后期。我们测量滞后时间为生长速率降到葡萄糖最大值以下的时间。该模型预测的滞后期在450 - 475分钟之间,与实验观测到的滞后期在470 - 490分钟之间很好地吻合。(从数据中确定滞后期持续时间的准确性明显受到测量频率的限制,在这种情况下,每隔30分钟进行一次声移前后,每隔10分钟进行一次位移)。
当菌株1开始消耗乳糖时,其蛋白质质量分数调整以优化乳糖消耗,最明显的是乳糖特异性酶的质量分数。菌株1在乳糖耗尽时停止生长,大约在12小时,它的蛋白质质量分数停止变化。模型预测的乳糖浓度(12小时为零)与实验数据(12小时后乳糖未完全耗尽)之间存在差异。当微生物进入固定阶段时,必须表达在营养剥夺条件下生存所需的不同蛋白质(Jaishankar and Srivastava 2017)。我们在模型中没有考虑到这一点,因为我们主要关注于描述滞后阶段,这可能解释了观察到的差异。
从图6a可以看出,我们的描述捕捉到了大肠杆菌葡萄糖-乳糖二联酶非平凡生长曲线的所有主要特征。使用我们的相当基本的模型,以最小的拟合和不需要引入人工滞后参数,可以准确地再现滞后相位和双声位移。生长的所有阶段,包括初始滞后和双氧移,都是由微生物蛋白质组的结构决定的。
我们现在提出了一个敏感性分析的结果,看看拟合参数的变化是如何影响模型预测的。
参数、、和被确定为最适合Erickson等人(2017)的数据和我们的实验数据。为了一致性,除了对数相产率和外,所有参数(拟合的和从文献中取的)在两个模拟中都具有相同的值。这是因为产量取决于OD600与g/L生物量的比例,这在Erickson等人(2017)的实验和我们自己的实验之间会有所不同。然而,我们确实在两个模拟中保持了相同的比率。
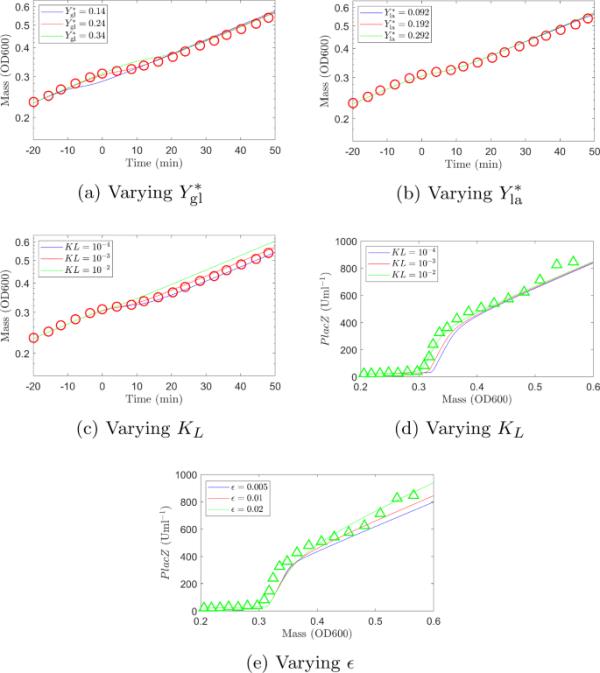
不同拟合参数值时数值解的比较(实验数据用红色圆圈表示(生物量),绿色三角形表示(PlacZ浓度))。a拟合值,用红色表示。减少(蓝色表示)减少了葡萄糖上的生物量增长,使双氧移的时间提前到最小值。相反,增加(绿色表示)增加了葡萄糖上的生物量增长,双氧移发生的时间推迟到最小值左右。减少(蓝色表示)或增加(绿色表示)对预测的增长曲线几乎没有影响。c, d拟合值,用红色表示。还原(用蓝色表示)意味着葡萄糖水平必须达到较低的值才能表达乳糖特异性酶。这增加了音频滞后的长度。相反,增加(绿色显示)意味着乳糖特异性酶在较高的葡萄糖水平下表达,从而缩短了双氧滞后。选择的拟合值是对生长曲线和酶表达水平曲线的最佳拟合。e拟合值,用红色表示。还原(蓝色部分)会更快地降低乳糖特异性酶的生成速率。相反,增加(绿色显示)意味着乳糖特异性酶的生产速度越高,持续时间越长(在线彩色图)
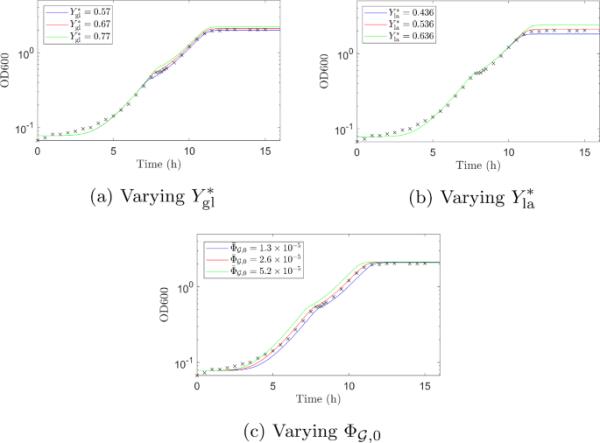
拟合参数值变化时数值解的比较(实验数据用黑叉表示)。a拟合值,用红色表示。降低对数相产量(用蓝色表示)会降低生物质浓度。相反,增加对数相产量(绿色部分)会增加生物质浓度。b拟合值,用红色表示。减少对数相产量(用蓝色表示)会降低双氧转换后的生物量浓度。相反,增加对数相产量(绿色部分)会增加双氧转换后的生物量浓度。c拟合值,用红色表示。减少(蓝色显示)降低了初始生长速率,增加了蛋白质质量分数达到最佳水平所需的时间,从而增加了初始滞后期的长度。最终的生物质产量也会降低。相反,增加(用绿色表示)增加了初始生长速率,缩短了初始滞后期,增加了最终生物量浓度。所示的所有情况下,生长曲线的定性行为都是相似的(在线彩色图)
最佳拟合值在附录g的表5中给出。表中的对数相产量是与Erickson等人(2017)数据拟合的结果;拟合我们的数据得到和。
图7和图8分别显示了模拟1和模拟2对不同拟合参数值的结果(同时显示了实验数据进行对比)。参数和拟合模拟1,因为在这种情况下,我们有酶表达水平和生物量的数据。该参数被拟合到模拟2中,因为它对模拟1的结果的影响可以忽略不计,因为没有初始滞后阶段。如上所述,对数相产率分别适合于两种模拟。
在图7和图8中,使用最佳拟合参数的预测曲线用红色表示。在每个子图中,一个参数是变化的,而所有其他参数是固定的(见附录G中的表4和表5)。正如预期的那样,改变葡萄糖和乳糖的产率会改变最终的生物量浓度;产率越低,最终生物量浓度越低,反之亦然(见图7a、b和图8a、b)。这在模拟2(图8a、b)中更为明显,其中模拟一直运行到乳糖耗尽为止。
这个常数决定了乳糖特异酶何时开始通过功能表达
并通过功能影响乳糖特异酶的生成速率
对于我们所拥有的值,乳糖特异性酶仅在非常低的水平上表达。只有当葡萄糖水平下降时,这种表达水平才会增加。减少会增加二元滞后期的长度,因为葡萄糖水平必须在乳糖开始消耗之前达到较低的值(图7c, d)。另一方面,如果增加,滞后期会缩短,极端情况()完全消除二元滞后期(葡萄糖和乳糖同时消耗)。该函数本质上是一个平滑的阶跃函数(for和for),其参数定义了阶跃的清晰度(当我们趋向于阶跃函数时,随着增加,从1到0的变化更平缓)。对于小的(一个陡峭的变化)乳糖特异性酶的生产从最大水平下降相当急剧时。随着产量的增加,产量下降的速度也随之减慢。这意味着越大,酶的产率越高,时间越长,如图7e所示,越大,乳糖特异性酶的表达水平增加的速度越快。
改变关键合成代谢蛋白的最小质量分数会改变初始滞后期的长度和最终的总生物量浓度(图8c)。该值越低,初始生长速率越慢,增加了蛋白质质量分数达到最佳水平所需的时间,从而增加了初始滞后期的长度。最终的生物量产量也越小。
双氧生长通常被认为是微生物最大化生长的过程,然而,在双氧滞后期存在显著的生长损失。在有效地消耗首选糖,最大化微生物的长期生长和在微生物适应使用次级糖的转换过程中失去生长之间存在权衡。在某些条件下,双耗行为是一种优势,而其他条件则有利于同时消耗资源?
当资源稀缺时,能够超越竞争对手的菌株将具有优势(Giordano et al. 2016)。在下文中,我们比较了具有相同初始生物量的两个菌株,因此我们将“更好”的生长策略定义为属于具有较高最终生物量浓度的菌株。
为了检验diauxie是否有利于生长,我们使用我们的参数化模型来模拟两种不同菌株的大肠杆菌的生长。我们设为双裂应变(与模拟1中的X相同),并引入不表现双裂的理论应变,。这种非双氧菌株同时消耗葡萄糖和乳糖,因此(这是3.3节中提到的极限)。假定所有其他增长参数与表4和表5中给出的相同。除了乳糖特异酶的初始条件外,这两种菌株的初始条件与附录G中描述的模拟1中使用的初始条件相同。因为我们有(表达前水平),因为我们有酶总是在这个菌株中表达(乳糖消耗不受非双氧菌株的抑制)。
我们首先使用我们的参数化模型来预测仅存在和仅存在时的增长曲线。然后,我们模拟两个菌株在竞争中的生长(在这个模拟中,我们假设初始生物量在两个菌株之间平均分配)。结果如图9所示。当只有一种菌株存在时(图9a),(蓝色)的最终生物量浓度高于(绿色):在这种情况下,有利于双生长。当葡萄糖存在时,双氧菌株会阻止乳糖的吸收,利用所有细胞的资源来代谢葡萄糖。非双氧细胞必须共享它们的资源来同时分解葡萄糖和乳糖,这降低了效率,降低了最终的生物量产量。然而,如果我们看一下双氧菌株和非双氧菌株竞争资源的情况,生长曲线如图9b所示,我们发现(绿色)超出(蓝色)。总生物量(黑色曲线)低于仅在(图9a中的蓝色曲线)上生长的情况,但高于仅在(图9a中的绿色曲线)上生长的情况。当两种糖都存在时,非双氧菌株(同时消耗两种糖)的生长速度比双氧菌株高,这使它具有竞争优势。此外,非双氧菌株在葡萄糖消耗时不会停止生长,没有双氧转移,这使它比双氧菌株有进一步的优势。
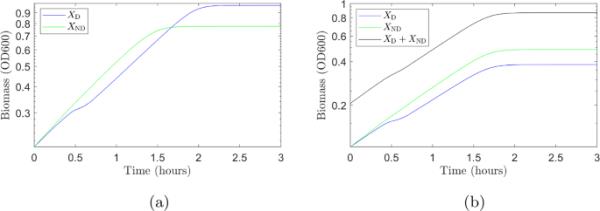
在0.3 g/L葡萄糖/2.0 g/L乳糖混合物上生长的大肠杆菌菌株生长曲线。a两个模拟中只存在一种应变(无竞争)的生长曲线:双应变(蓝色);非双氧菌株(绿色)。该菌株表现出双重作用,具有较高的最终生物量,因为它能够在乳糖的存在下有效地消耗葡萄糖。b两个菌株(蓝色)和(绿色)争夺资源的一个模拟的生长曲线。非双氧菌株胜过双氧菌株。最初具有比同时消耗葡萄糖和乳糖更高的生长速率。此外,它能够在葡萄糖耗尽时立即有效地消耗乳糖。这两个因素使它比双氧应变具有竞争优势(在线彩色图)
我们发现,当一株大肠杆菌在葡萄糖(0.3 g/L)和乳糖(2.0 g/L)的混合物中生长时,顺序消耗这两种糖是更好的,然而,当菌株竞争这些资源时,对菌株生长并不一定有益。为了研究不同的葡萄糖-乳糖混合物是否仍然存在这种情况,对一系列不同的葡萄糖和乳糖初始浓度进行了重复模拟。每次模拟运行,直到所有的糖被耗尽,并获得每个菌株的最终生物量浓度。计算了两菌株的最终生物量之比。非竞争性情况下的结果如图10a所示。对于大多数初始浓度的葡萄糖和乳糖,双氧菌株表现更好。只有当葡萄糖的初始浓度远高于乳糖的初始浓度时,非双氧菌株才具有较高的生物量。图10b显示了竞争情况下的结果。当菌株竞争相同的资源时,非共生菌株总是具有更高的最终生物量。
图9的结果表明,在0.3 g/L葡萄糖2.0 g/L乳糖的混合物中,双氧菌株的生长速率低于非双氧菌株,但生物量产量高于非双氧菌株。通过在葡萄糖和乳糖的初始浓度范围内进行模拟,结果如图10所示,我们发现,除了葡萄糖的初始浓度远高于乳糖的初始浓度外,我们有相同的情况:双氧菌株的生长速度低于非双氧菌株,但生物量产量高于非双氧菌株。我们推断,在非竞争环境中,增长量最大化是一种优势(Giordano et al. 2016),而在竞争环境中,增长率最大化是一种优势(Ibarra et al. 2002),增长量增长不是最优增长策略。
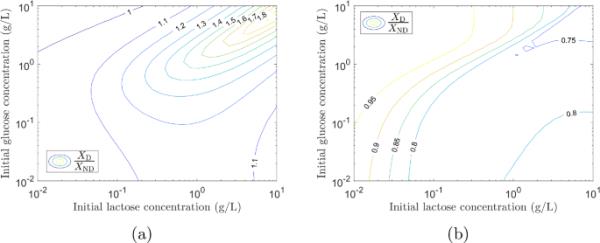
在葡萄糖/乳糖混合物中生长的两株大肠杆菌的比较,表现出双氧和没有双氧转移。a非竞争性模拟结果。模拟不同初始浓度的葡萄糖和乳糖的最终生物量比。对于大多数葡萄糖和乳糖的初始浓度,双氧菌株具有较高的最终生物量()。非双氧菌株只有在初始葡萄糖浓度远大于初始乳糖浓度时才有较高的终生物量()。b竞争性模拟结果。模拟不同初始浓度的葡萄糖和乳糖的最终生物量比。非有害菌株总是具有更高的最终生物量()(在线彩色图)
研究表明,细菌菌株(Spencer et al. 2007)和酵母菌株(Wang et al. 2015)可以进化成具有不同长度的双氧转换。当微生物受到环境频繁变化的影响时,其滞发期会逐渐变短,而在稳定的环境中,滞发期会变长(Chu and Barnes 2016)。
对于恒定的糖浓度,我们有稳定的生长环境。当糖被消耗时,生长环境随着葡萄糖/乳糖的消耗而变化,因此初始糖浓度越高,条件变化前的时间越长。因此,当两种糖的初始浓度增加时,可以认为环境在较长时间内是稳定的。图10a的结果表明,随着初始糖浓度的增加,生长的优势增加(增加)。我们的模拟结果与实验证据定性地一致,即具有长双氧滞后的细菌(Spencer et al. 2007)和酵母菌株(Wang et al. 2015)在稳定环境中表现更好,而具有短双氧滞后(或无双氧滞后)的细菌株在变化的环境中表现更好。
发表评论
评论列表
质量分数一书深入浅出,为理解与运用质量管理提供了实用指南。