非牛顿纳米流体在具有粘性耗散的指数拉伸薄片上的流动:基于apell - changhee多项式的SCM数值研究
21
2025-02-07
研究一类耦合复mKdV (CCMKDV)方程的初值问题
$ $ \{对齐}开始u_ {t} + u_ {xxx} + 6 \ bigl(\ \绿色绿色u ^{2} + \绿色v \绿色^ {2}\ bigr) u_ {x} + 6 u \ bigl(\ \绿色绿色v ^ {2} \ bigr) _ {x} = 0, \ \ &v_ {t} + v_ {xxx} + 6 \ bigl(\ \绿色绿色u ^{2} + \绿色v \绿色^ {2}\ bigr) v_ {x} + 6 v \ bigl(\ \绿色绿色u ^ {2} \ bigr) _ {x} = 0, \{对齐}$ $由Yang(可积和不可积系统中的非线性波,2010)提出,该问题与一个\(4 \ × 4\)散射问题有关。基于矩阵谱分析,构造了一个四阶矩阵黎曼-希尔伯特问题。通过求解一类特殊的非正则零Riemann-Hilbert问题,给出了CCMKDV系统的n孤子解。此外,单孤子解用图形显示。
在非线性波动理论中,可积非线性方程起着重要的作用,包括KdV方程、非线性Schrödinger方程、sin - gordon方程、修正KdV方程等。这些可积系统通常具有丰富的数学结构,如Lax对公式和丰富的守恒定律。为了探索这些模型的精确解,已经开发了大量有效的方法,如逆散射变换(IST)方法[2,3]、Hirota双线性方法[4]、Bäcklund变换方法[5]、Dressing方法[6]等。在IST方法的初始版本中,必须求解Gel 'fand-Levitan-Marchenko (GLM)积分方程,这不是一项容易的任务。后来,IST的简化版本被开发出来,被称为Riemann-Hilbert (RH)方法[1,7]。此后,许多研究者利用RH方法找到了一些物理上重要的可积偏微分方程的孤子解[8-18]。近年来,RH方法也被证明适用于研究一些可积非线性方程初边值问题解的渐近行为[19-23]。关于最近用RH方法构造的关于高阶极点的孤子解,参见[24,25]。
mKdV方程
(1)是物理学中一个重要的可积模型,它最初被提出用来描述一些非调和晶格中的声波以及冷无碰撞等离子体中的Alfven波[26]。随后,许多研究者通过广义Darboux变换方法、IST方法、Hirota双线性方法等方法研究了mKdV方程的多孤子、守恒量、代数-几何解、异常波以及一些耦合mKdV方程[11,12,27 - 31]。研究者还利用Fokas统一变换方法[21,22,32]和矢量mKdV方程的摄动理论[33]研究了耦合mKdV方程的初边值问题。最近,用非线性最陡下降法研究了耦合mKdV方程的长时间渐近性质[34]。解决方案的分类见[35]。
本文的主要目的是研究一个CCMKDV系统[1]
(2)在RH公式中,其中,表示复杂的场包络。这些术语涉及并解释了色散效应,色散效应会影响波包随时间的传播。同时,耦合项描述了两个波分量和之间的相互作用。很容易看出,当,该系统化为mKdV方程(1)。矢量mKdV系统的孤子解已经用Hirota双线性方法[36]和IST方法[29]进行了研究。其他一些耦合的mKdV系统也使用RH公式进行了研究[30,31],但我们注意到这个CCMKDV系统(2)不能被[30,31]涵盖。据我们所知,CCMKDV系统(2)的RH问题之前还没有研究过。
本文安排如下:在第2节中,我们首先处理CCMKDV系统(2)的Lax对,经过一些谱分析,我们给出了x部分谱方程的Jost解的解析性质。在第3节中,我们将为这个CCMKDV系统制定相应的RH问题。在第4节中,我们将用简单的零来解决RH问题。通过限制无反射情况和重构势,我们将构造方程(2)的n孤子解。通过选择合适的参数,我们将图形化地展示CCMKDV系统的单孤子解的行为。最后一节论述了本文的主要内容。在第2节中,我们首先处理CCMKDV系统(2)的Lax对,经过一些谱分析,我们给出了x部分谱方程的Jost解的解析性质。在第3节中,我们将为这个CCMKDV系统制定相应的RH问题。在第4节中,我们将用简单零来解决RH问题,并通过限制无反射情况和重构势,构造方程(2)的n -孤子解。通过选择合适的参数,我们将图形化地展示CCMKDV系统的单孤子解的行为。最后一部分是结论部分。得出结论。
在本节中,我们重点研究CCMKDV系统(2)的散射问题,并研究其矩阵Jost解。
Yang[1]指出,CCMKDV系统(2)在以下意义上是Lax可积的
(3) (4)其中ω是一个谱参数,是一个矩阵函数。矩阵σ, Ũ, Q, Ṽ定义如下
在这
其中†表示矩阵的厄米共轭。很容易发现Ũ满足以下对称条件
(5)接下来,我们总是假设势函数满足零边界条件,即
为了研究方程(2)的局部解,我们简单地引入了一个新的矩阵谱函数
(6)则(3)、(4)可改写为
(7) (8)在哪里。
在散射问题中,我们首先研究了方程(7)的Jost解满足
(9)其中I为单位矩阵,下标in表示在x轴的哪一端设置边界条件。众所周知,
(10)式中为矩阵J的行列式,表示矩阵的迹。由于,它产生了
(11)在构造RH问题之前,只要建立Jost解和散射矩阵的解析性质就足够了。为了达到这个目的,让我们把它分成列向量,即。通过Volterra积分,可以将第一列改写为:
(12)通过对Jost解解析性质的类似论证[1,8],可知它在上半平面上是解析的,在实轴上是连续的。同理,,,在上半平面上是解析的,在实轴上是连续的,而,,在下半平面上是解析的,在实轴上是连续的。
表示,很容易看出两者都是(3)的基本解,因此它们与散射矩阵线性相关。这是
(13)由式(11)和式(13)可知
(14)由式(13)可得
(15)这表明在导出项的解析性质之前,我们需要研究的解析性质。为此,我们从(7)的伴随谱方程开始。
(16)可以简单地找到满足式(16),其中被划分成行
(17)通过类似的论证,我们发现,,,是解析的in,而,,是解析的for。由于和的解析性,可以得到,,,在上半平面上是解析的,,,,在,,,,,,,上是解析的,仅对有定义且连续。
让我们从和的对称条件开始。首先,从(7)和(5)可以很容易地得出
(18)因此两者都解决了伴随谱问题(16),它们也趋向于单位矩阵为。因此,
(19)通过类似的论证,我们得到
(20)接下来,我们将制定RH问题。为了实现这一点,我们引入了下面的矩阵函数
(21)在哪里
(22)很明显,在(7)中是解析的,求解了谱方程(7)。
(23)因此
(24)其中,。根据(23),我们得到,。为了得到in的解析对应项,我们研究了以下矩阵函数:
(25)从(23)可以清楚地看出,它在(7)中是解析的,并且也求解了谱方程
(26)很容易得出
(27)还有,。
现在我们准备借助和来表述RH问题,即
(28)跳跃矩阵如下所示
(29)此外,由(19)、(23)、(26)可知
(30)我们用简单零来解决RH问题(28),即假设并承认简单零,对于多零情况,我们参考[37,38]。由式(24)和式(27)可知,和的零个数相同,而且,如果是的简单零,则必然是的简单零。因此,假设是的简单零,那么我们可以简单地表示by的零。那么一定存在一个列向量满足
(31)求(31)的厄米共轭
(32)由于……,我们
(33)为简单起见,我们表示
(34)接下来,我们将找到和的显式表达式。由式(7)、式(21)、式(31)可知
(35)通过类似的论证,我们有
(36)因此
(37)其中是一个复常数向量。
众所周知,通过消除零和Plemelj公式[39],不规则RH问题(28)可以求解如下[1]
(38)其中M是一个可逆矩阵,其元素定义如下
(39)为了得到耦合的mKdV方程(2)的孤子解,将解展开即可,
(40)注意,孤子解对应于散射数据消失的情况,即。将(40)代入谱式(7),得到
(41)的收益率
(42)式中表示矩阵的第-个元素。通过直接计算,由式(38)可得
(43)因此,耦合的mKdV方程(2)的n孤子解为
(44)在哪里和。
具体地说,当,我们可以得到u, v的显式表达式。为此,我们引入以下符号
(45)其中()为复常数,argA表示a的参数。由式(37)和式(45)可知
(46)鉴于(38)、(40)和(41),人们得到
(47)因此,我们有
(48)CCMKDV系统(2)的单孤子解如下
(49)此外,复常数,,满足
设,,,我们在图1中绘制了CCMKDV系统(2)的单孤子解的图形。
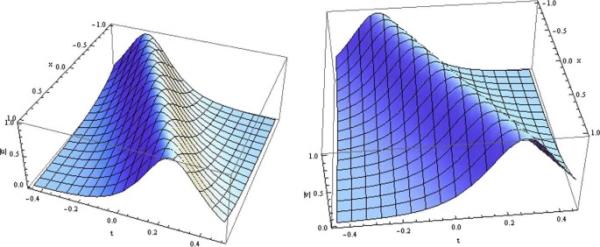
u和v中的单个非简并孤子,相关参数为:,
设和,则CCMKDV系统(2)的双孤子解为
(50) (51)在这
(52)由于……,我们
(53)此外,通过选择合适的参数,双孤子相互作用如图2所示。
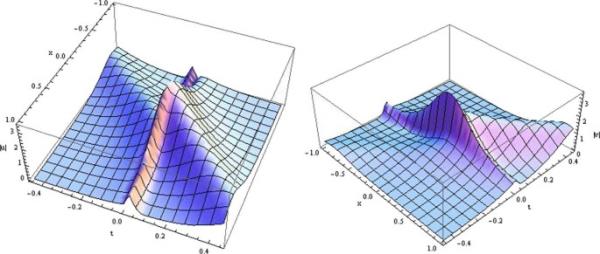
u和v通过(50)-(52)的双孤子相互作用,相关参数为:,,,
本文研究了CCMKDV系统(2)。通过分析其谱问题,构造了关联矩阵RH问题。通过消除零和Plemelj公式[39],我们用简单的零解决了RH问题。随后,我们给出了式(2)的n -孤子解的公式。具体地说,我们明确地给出了单孤子解,并用图形表示了单孤子解的动力学行为。我们注意到,我们只处理势函数满足某些零边界条件的情况。对于势不服从这些消失条件的一般情况,可以得到更一般的解,这可以在将来进行研究。
发表评论
暂时没有评论,来抢沙发吧~