自增强PLA复合材料固结过程中的温度对其力学性能有显著影响。本文通过单纤维试验,研究了固结温度和加工温度对熔融纺丝高取向聚乳酸纤维性能的影响。结果表明,PLA纤维的杨氏模量和破坏应变随固结/加工温度的增加而增加,而强度下降的幅度更大。利用这些数据和早期的研究结果,证明了自增强PLA复合材料的拉伸性能与加工温度的依赖关系可以直接从单个PLA纤维性能作为加工温度的函数来预测。如果PLA纤维和自增强PLA复合材料的拉伸性能使用相同的交叉头速度或应变速率测量,则该预测成立。
随着人们对可持续和环保材料意识的提高,生物塑料正获得越来越多的兴趣。聚乳酸(PLA)是从玉米或甜菜等可再生资源中提取的,可能是应用最广泛的生物塑料/生物聚合物。与其他生物塑料相比,它具有相对吸引人的力学性能,可生物降解,工业生产能力高[1]。然而,由于与石油基聚合物相比,PLA的机械性能较低,因此主要用作一次性或包装材料[2]。
提高纯聚乳酸力学性能的一种方法是通过添加各种形式的纤维素等增强剂来开发聚乳酸复合材料[3,4,5,6]。然而,即使添加了生物基增强材料,也不一定意味着这些复合材料的环境性能与纯PLA的环境性能相等,即复合材料的生态性能可能更低[7,8,9]。
另一种方法是基于自增强复合材料的概念,其中基体用由相同聚合物制成的定向纤维增强,但熔化温度更高[10,11,12]。第一个自增强复合材料是基于聚乙烯[13],后来这个概念被扩展到各种其他材料体系,如聚丙烯[14,15,16,17],聚酰胺[18],芳纶[19]和纤维素[20,21,22]。然而,直到最近才有有限的论文将这一概念应用于开发基于可再生资源的完全可生物降解的自增强PLA复合材料[9,23,24,25]。
自增强复合材料的机械性能可以通过增加增强材料中聚合物链的取向来增强[26],即开发高刚度和高强度的纤维。通过溶液纺丝生产的定向PLA纤维可以具有非常高的性能,例如抗拉强度为1 GPa[27]或2.1 GPa,杨氏模量为16 GPa[28]。然而,商用PLA纤维通常通过熔融纺丝生产,以实现更高的生产率,并避免使用溶剂[2]。熔融纺PLA纤维性能较低;所报道的强度为280 ~ 870 MPa,杨氏模量为5.2 ~ 9.2 GPa[2,29,30,31,32]。所报告的强度和模量值的广泛范围源于聚合物纤维性能对以下因素的强烈依赖:a)所使用的PLA等级,b)挤压工艺参数,以及c)拉伸参数(图1a)。制造参数的优化一直是一个活跃的研究课题,包括PLA[2,25,27]。
纤维制造完成后,自增强复合材料的生产通常涉及热压固结[9,25]。这个过程包括加热材料以熔化PLA,这将形成基体,而不是PLA纤维。然而,在此过程中,PLA纤维也被加热,其性能将发生显著变化。因此,决定自增强PLA复合材料性能的纤维性能通常与通常测量的性能(拉伸后但复合加工前)有很大不同。本研究的目的是研究自增强复合材料的加工条件对PLA纤维性能的影响,进而对PLA自增强复合材料的性能产生影响。
本文的结构如下。首先,在室温下使用不同的测量长度和测试速度对纤维强度分布进行了统计分析。然后,在不同的工艺温度下,在不同的测试速度下,在固定的测量长度下,测量纤维的性能。应该强调的是,PLA纤维的拉伸比是保持恒定的。然后讨论了这些结果对复合材料性能的影响。最后,总结了主要研究结果。
从Total Corbion PLA购买了一种高熔点、中等流动的均聚物PLA (L130 PLA级)。PLA材料首先复合,然后使用试验线熔融纺成多纤维纱线(图1a)。抽签比为2.76。更多关于PLA纱线制造过程的细节可以在其他地方找到[33]。当前工作的重点是复合工艺参数(制造自增强PLA复合材料)对PLA纤维性能的影响,以及随后对复合材料性能的影响,即起点是在PLA纤维熔融纺丝并从PLA化合物中提取之后。
PLA纱线生产完成后(图1a),使用定制的绕线机将纱线从线轴上绕到金属框架中(见图1b)。随后,将框架放置在真空和温度等于35℃的烤箱中过夜,以干燥PLA纤维。
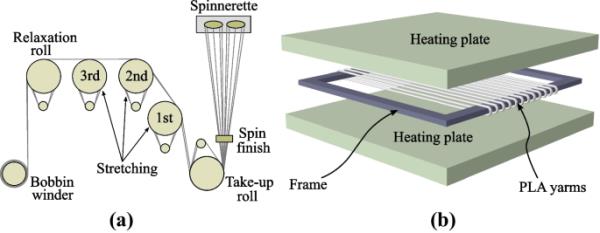
PLA纱线的固态拉伸试验线及压固原理图
PLA纱线然后在一个定制的压制设备中使用两步工艺压制巩固。在压制设备的第一部分,将缠绕PLA纱线的机架在真空下加热10分钟至工艺温度。加热是通过两块金属板的接触施加的,如图1b所示。随后,在第二步中,将框架快速移动到压榨设备的第二部分,并在2 MPa的压力下在1分钟内冷却到30℃。这些工艺参数与用于制造自增强PLA复合材料的参数相同[25,33,34],因此近似于PLA纤维在复合材料制造过程中所经历的条件。工艺温度从155℃变化到180℃,增量为5℃。在155℃到175℃的工艺窗口中,PLA纤维不熔化,而在180℃时PLA纤维熔化。值得注意的是,在目前的研究中,与复合材料制造的情况相比,框架中的纤维较少[25,33,34],纤维承受的压力可能小于2兆帕。然而,可以认为,施加压力的电位差对报告的结果没有显着影响。
压实后,从PLA纱线中小心地提取单个PLA纤维,以防止对PLA纤维的任何损坏。对于不同的工艺温度,除了180℃的情况下,提取单个纤维是直接的。在180℃的工艺温度下,只有有限数量的纤维被提取出来,因为在这个温度下纤维会融化并相互粘在一起。
在Favimat & Robot单纤维试验机(Textechno H. Stein GmbH & Co. KG)上测试了单PLA纤维的张力。单个纤维首先被装入一个杂志(最多25个样品),每个纤维的底部附有100毫克的预张力。然后,机器人将一根一根的纤维移动到测试室。首先夹紧每根纤维,然后施加0.5 cN(小规格长度)和1.5 cN(大规格长度)之间的预张力。随后,按照ASTM标准D1577-07[35]使用振动法测量纤维的线密度(每长度的质量)。在这种方法中,共振频率最初是在恒定的规长和预张力下测量的,从而可以评估线性质量密度。在线密度测量之后,对纤维进行张力测试。在所有力学试验中,施加0.1 cN的预张力,并记录荷载-位移曲线。利用线密度和记录的载荷,可以计算出纤维的应力。
论文中检查纤维强度分布的部分,纤维没有被压实,测量长度从10毫米到75毫米不等。进行了两组实验。在第一组中,所有仪表长度的交叉头速度为20毫米/分钟。在第二组中,根据测量长度的不同,十字头速度变化,使其具有等于0.25秒的标称应变速率。在每个测试条件下,大约测试了100根纤维。这些纤维是从不同的线轴中随机选择的,以更准确地捕捉纤维强度的变化。
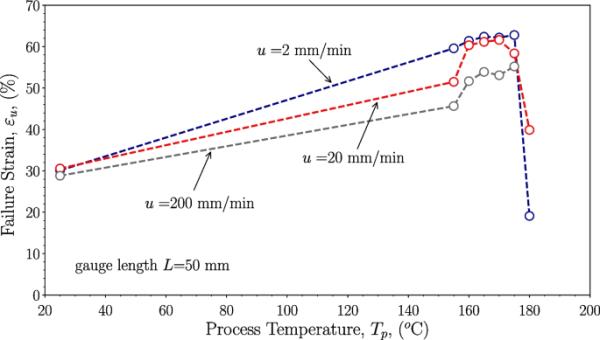
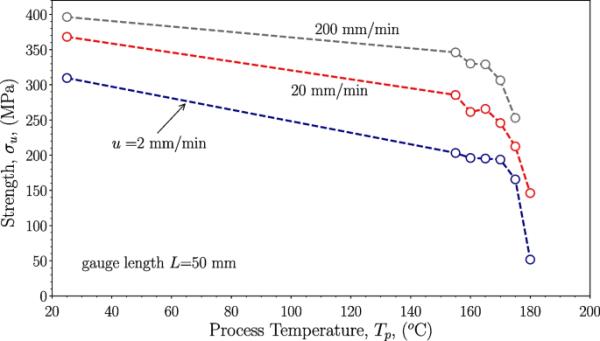
为了研究压实温度对纤维力学性能的影响,规范长度为50 mm。分别在0.2、20和200 mm/min的固定十字头速度下对不同的压实温度进行了试验。在大多数情况下,大约测试了50根纤维。所有的纤维都是从同一个筒子上取下来的。
纤维的强度分布,特别是脆性纤维的强度分布,用Weibull分布来描述[36],它通常可以是两个或三个参数的分布[37,38]。设阈值应力为零,则在均匀应力下,两个参数的分布为:
(1)式中为长度为L的纤维在应力作用下破坏的概率。特征长度记为。威布尔模量为m,特征强度为。
为了实验确定m和,将设为L的Eq. 1改写为:
(2)然后,用直线拟合实验数据。由直线的系数可以确定威布尔参数[39]。则由m和,可计算出纤维的平均强度,,
(3)这里是函数。式1中第i根纤维的失效概率为:
(4)其中N为特定测试条件下成功测试的光纤总数。在应用公式4之前,纤维从最低强度到最高强度进行分类。在对纤维进行分类后,还可以计算出中值强度。除了Eq. 4之外,还提出了许多其他的概率估计[40,41]。一些估计器比其他估计器偏差更小[40,42,43],然而,对于本研究的目的,Eq. 4足以确定PLA纤维的威布尔参数。
除了利用威布尔分布外,纤维强度也具有高斯分布的特征。威布尔分布主要适用于脆性材料,而对于本研究中使用的PLA纤维等延性材料,可以使用高斯分布或正态分布。
采用温度调制差示扫描量热法(DSC 214 Polyma, NETZSCH-Gerätebau GmbH)测量PLA纤维的热转变。样品约为10 mg,加热温度为25℃至200℃,升温速率为5℃/min,振幅为0.8℃/min,周期为60s,作为吹扫气体。
PLA纤维的结晶度(%)通过以下方法计算:
(5)其中为熔融焓,为冷结晶焓,由于在测量中没有观察到冷结晶,因此假设为零。为100%结晶PLA的熔化焓,根据前人的研究[44,45]设为93.0J/g。
图2显示了两种不同厚度的威布尔图,L分别等于15和25毫米。对于每个量规长度,给出了两组数据,一组是在恒定的交叉头速度下获得的,另一组是在恒定的标称应变率下获得的。从所有量规长度的图中,可以得到表1和表2的数据。
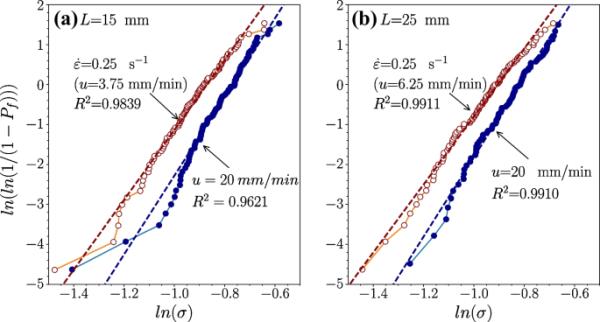
威布尔图以20mm /min和0.25 s的速度进行,量规长度为15mm,量规长度为25mm
表1显示了PLA纤维在恒定横头速度u = 20 mm/min且与规长L无关的情况下的Weibull参数,即对于较大的规长,应变率较低。中位强度是纤维按2.2.1节所述进行分选后中位纤维的强度。可以看出,中位强度与平均强度之间的差异在L = 75 mm时约为3.3%,在L = 15 mm时约为0.4%。特性强度大于或适用于所有规长。在10 mm处差异最大,约为6%。最小威布尔模量m为7.2,为10 mm。对于所有量规长度,威布尔模量都很大,其次与高斯分布的标准差有一一对应关系。最小的标准偏差为60mm,对于这个量规长度,测量了最大的威布尔模量。
表2与表1类似,不同之处在于,对于每个量规长度,调整十字头位移以达到标称应变率,等于0.25 s,即。可以看出,与表1相比,威布尔模量和标准差的变化较小。中位强度近似等于平均强度;除L = 50mm时差异3%外,其余均小于1%。如表1所示,特征强度高于中值强度和平均强度;对于所有测试的量规长度,差异约为5%。
通过将中值应力(表1和表2)作为规范长度的函数进行线性拟合,可以获得更准确的威布尔模量估计(见图3)。在恒定交叉速度下测试的纤维的威布尔模量为9.3,而在恒定标称应变速率下测试的纤维,威布尔模量为15.5。
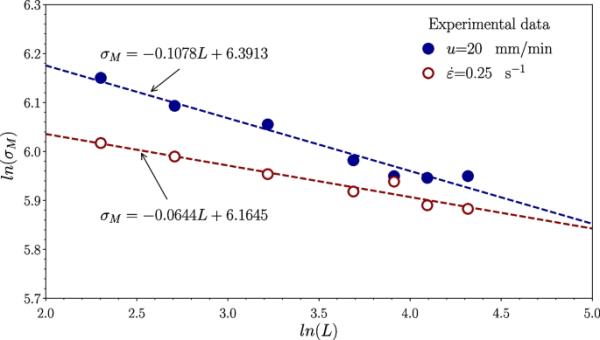
在恒交叉头速度和名义应变下,拉伸后熔融纺PLA纤维的中值应力随规长函数的对数图(见表1和表2)。直线斜率为
图4总结了拉伸后熔融纺丝PLA纤维的杨氏模量和失效应变随规范长度的函数。正如预期的那样,杨氏模量与规范长度无关,约等于7.37 GPa(当u = 20 mm/min或0.25 s时),破坏应变随规范长度增加而增加。然而,破坏应变对规范长度的依赖性较弱。由图4b可以看出,当L = 10 mm时,平均破坏应变约为33.8%,当L = 75 mm时,平均破坏应变约为29.1%。
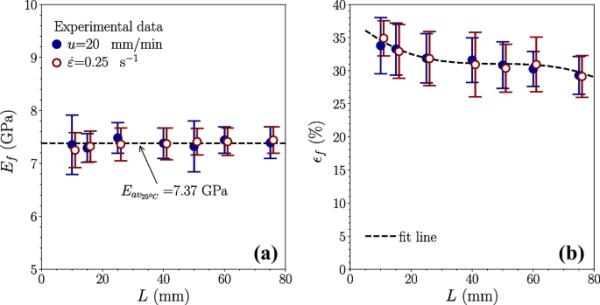
恒交叉头速度和恒标称应变速率下熔融纺PLA纤维拉拔后的杨氏模量和破坏应变。误差条基于标准差
图5显示了在工艺温度下,熔融纺丝拉伸PLA纤维在压实前后的DSC曲线的典型示例。工艺温度影响的DSC结果如表3所示。可以看出,随着工艺温度的升高,起始温度、熔融温度和结晶度均逐渐升高。当温度接近175℃时,增加的速率明显更高。超过这个特征温度,由于PLA纤维在加工过程中的熔化,起始温度、熔化温度和结晶度显著下降,这从表3中可以清楚地看出。
熔融纺丝和拉伸PLA纤维的典型DSC曲线以及PLA纤维在等于165℃和175℃时的后处理
加工温度对纤维杨氏模量的影响如图6所示,对纤维强度的影响如图7所示,对纤维破坏应变的影响如图8所示。在这些图中,每个符号表示从几次试验中获得的平均值(见表4)。杨氏模量、强度和破坏应变的结果也分别列在表5、表6和表7中,以便更清楚地观察到标准差。
加工温度和交叉头速度对PLA纤维杨氏模量的影响。量规长度L为50毫米
加工温度、、和交叉头速度对PLA纤维强度的影响。量规长度L为50毫米

加工温度、、和交叉头速度对PLA纤维强度的影响。量规长度L为50毫米
可以看出,PLA纤维的杨氏模量随着加工温度的增加而增加,在160-165℃之间达到最大值,相对于未加工的纤维增加了约10%。较高的加工温度导致较低的杨氏模量,而等于180℃(高于纤维熔化温度)的杨氏模量等于3.62 GPa(对于u = 2 mm/min),这大致等于PLA材料的杨氏模量(见第2.1节),而没有任何拉伸。加工温度对纤维强度的影响较大。当加工温度为165℃时,纤维强度降低1/3,而当加工温度为175℃时,纤维强度降低2倍。纤维的破坏应变(图8和表7)随着工艺温度的增加而增加,达到175℃。有趣的是,PLA纤维的破坏应变比拉伸后未经过后处理的纤维高近2倍。
从上述结果可以看出,即使十字头速度从2 mm/min增加到20 mm/min,也可以观察到十字头速度对所有特征力学性能(杨氏模量、强度和破坏应变)的强烈影响。这一点的重要性将在下一节中讨论。
可以使用上一节给出的结果来预测单向自增强PLA复合材料的力学性能。在3.1节中,正如预期的那样,高取向PLA纤维的失效并不取决于缺陷。然后,可以得到PLA纤维的平均应力-应变曲线(基于工程应力和应变)作为单个纤维测试的平均值,如图9所示。图9为经u = 20mm /min,拉伸后未加工的纤维。从表4可以看出,用45根纤维计算PLA纤维的平均应力-应变曲线。随着施加位移的增加,平均应力-应变曲线基于单个纤维试验次数的持续减少,因为有些纤维比其他纤维更早断裂。
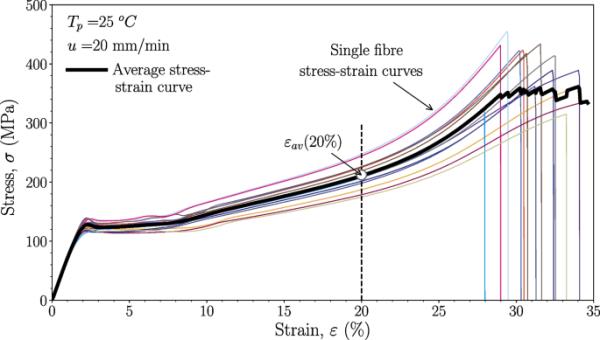
单个单纤维测试的平均PLA纤维应力-应变曲线。规长L为50mm,横头速度u为20mm /min
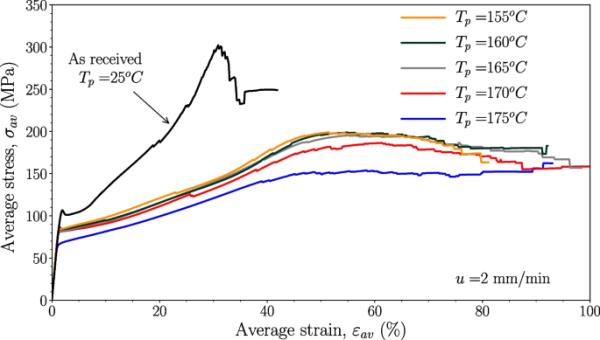
在不同的处理温度下重复图9中描述的过程,结果绘制在图10中。可以清楚地看到,热处理后的PLA纤维平均应力-应变曲线与拉伸后的PLA纤维平均应力-应变曲线有显著差异。更重要的是,PLA纤维的平均应力-应变曲线与单向PLA自增强复合材料的应力-应变曲线在质量上非常相似[34]。

不同加工温度下PLA纤维的平均应力应变曲线。量规长度L为50mm,横头速度u为2mm /min
利用平均PLA纤维应力-应变曲线的线性部分或表5的结果,使用混合规则预测自增强复合材料的杨氏模量,并与实验测量结果进行比较[34]。需要说明的是,在文献[34]中报道的实验中,纤维体积分数为50%。因此,在混合规则中,假设纤维体积分数等于50%,PLA基体的模量等于3.62(表5 - = 180℃)。预测结果如表8所示。可以看出,预测与测量是一致的。因此,很明显,不应该使用拉伸后的纤维性能(例如,忽略复合材料制造或加工过程中发生的变化)来预测或理解PLA自增强复合材料的行为。
以类似的方式,通过利用图10的结果作为表9中实验的函数并与之比较,可以预测单向复合材料的强度。如前所述,假设纤维体积分数为50%。此外,根据早期的研究结果[33],PLA基体在低施加应变下以脆性方式早期失效,因此复合材料的强度主要取决于PLA纤维。因此,单向纤维复合材料的强度可以通过将图10中的最大应力乘以0.5(纤维体积分数)来估计。从表9可以看出,考虑到纤维体积分数、工艺温度()的不确定性以及PLA纤维制造过程中的变化(熔融纺丝和拉伸),预测结果与实验结果一致。
如果从表6中取纤维强度,则可以获得类似的强度预测,但是,这种方法不太严格。在考虑破坏应变时,这一点变得很明显。表6的破坏应变在155-175 c范围内约为60%。Beauson等[34]发现,类似的破坏应变在90 - 150%之间。图10的破坏应变在90 ~ 100%之间,与实验测量值更接近。人们应该期望增加测试纤维的数量(表4)将导致与实验更好的一致性,因为破坏应变取决于具有较高应变到破坏的单个PLA纤维。
通常,单纤维测试或特别是纱线测试是在相对较高的交叉头速度下进行的,在100到500毫米/分钟之间。另一方面,复合材料在较低的速度下进行测试,速度为1 ~ 5 mm/min。图11显示了三种不同的十字头速度(2、20和200 mm/min)下拉伸后和165℃下加工后的平均纤维应力-应变曲线。可以清楚地看到,交叉头速度的影响是显著的。如果考虑在165℃下加工的纤维,按照上述方法,当u = 200mm /min时,预测复合强度为149.8 MPa。该值明显高于实验测量值(93 MPa,表9)或使用u = 2 mm/min的预测值(97.7 MPa,表9)。因此,在低速下测试聚合物纤维是有利的,与复合材料测试中使用的速度相对应,以便直接预测复合材料的行为,而无需在复合材料水平上进行实验。

测试速度对165℃拉伸后和加工后PLA纤维平均应力-应变曲线的影响。规长L为50mm
加工温度高于PLA的玻璃化转变温度,约为60℃。热处理或退火可以同时促进各种微观结构效应,包括聚合物链弛豫、取向和结晶(表3),这反过来又显著影响定向PLA纤维本身的力学性能(见3.3节)及其自增强复合性能(见4.1节)。要深入了解这些微观结构变化之间的相互作用,需要在分子水平上进行建模,这超出了当前工作的范围。在这里,应该强调的是,增加加工温度会导致杨氏模量和破坏应变(变形增加)的增加,但同时纤维强度下降得更剧烈。
通过单纤维试验,研究了加工温度对熔融纺丝取向PLA纤维力学性能的影响。结果表明,随着加工温度的升高,PLA纤维的杨氏模量和失效应变均有所增加,但强度的降低幅度较大。经过一定的加工温度后,PLA纤维完全熔化,性能降至非晶态PLA的水平。研究还表明,一旦定向PLA纤维的性能已知,就有可能预测单向PLA自增强复合材料的拉伸性能。这种预测要求纤维性能考虑到加工温度的影响,并且纤维和复合材料都在相似的应变速率下进行测试。
发表评论
暂时没有评论,来抢沙发吧~